【中学受験】2024年洛南中算数の大問5を解いてみた

時間がある時に、「中学への算数」の増刊である「必ず解きたい算数の100問」を次男とやっています。

2024年と2023年の中学入試問題から解いていて面白く学習効果が高い問題が選出されています。

解説もさまざまな塾講師が執筆していて、単なる解答ではなく、その背後にある出題意図まで踏み込んでいてくれます。

中学受験で同じ問題は出ないとは思いますが「背後にある出題意図」を理解しておくと、姿は変えているが似たような問題を見抜くのに役立ちます。

だいたい週に3日くらい、1日1問ペースで解いています。

問題は現時点でギリギリ解けるか解けないかをピックアップしています。

今回は2024年洛南中学の大問5の場合の数をしてみました。

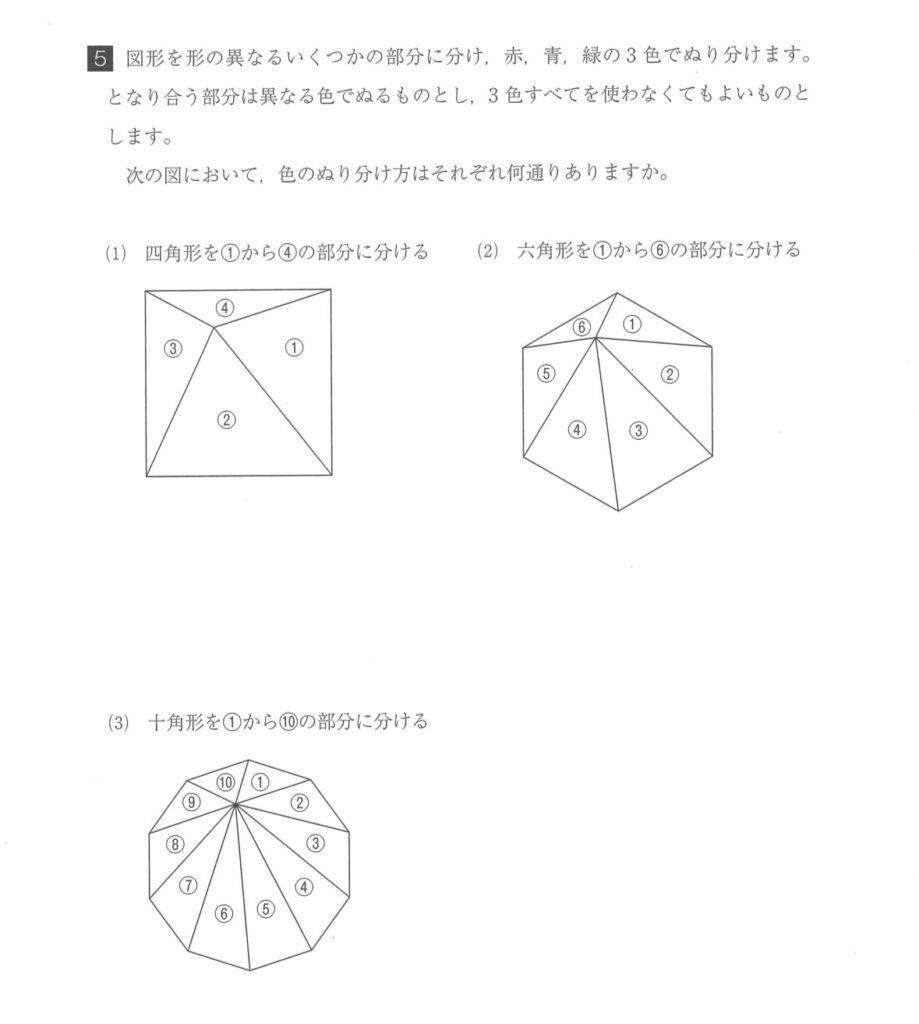
もうちょっと難易度を上げれば、大学受験で出題されてもおかしくない問題な感じがします。

（1）と（2）は力技で解けるので、次男もなんとか時間内に解けました。

毎回（1）ごとに3〜5分の時間制限でやっています。

これは3問✖︎4分＝12分でやっています。

（3）が（1）と（2）の応用なのですが、なかなか気づきません。

N角形のN分割の塗り分け問題。

法則に気づかないと解けないのですが、時間内で法則に気付ける子はかなり少ないと予想します。

一方で、一度でも解いたことがある子は余裕だったと思います。

まぁ、全ての問題に言えるのですが、

過去にどれだけ問題を解いてきて習得してきているか

が大事です。

限られた時間内で初見で正答に辿り着くには限界があるので、やはり天才でない限り、日頃からたくさんの問題に触れることしか勝ち目はありません。

この問題集は一問一問がヘビーなのですが、塾がかなり厳しくなる6年生までにできる限り進めておきたいとは思っています。

が、まだ20％弱。

全ては終わらないとは思いますが、Bランクはせめて網羅したいとは思っています。

（注）A簡単、B普通とC難しいに分かれていますが、ほとんどがBかCです。

これだけやっても、テストで高得点を維持するって困難なんですよね。